Phương pháp giải:

Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông

Lời giải chi tiết:

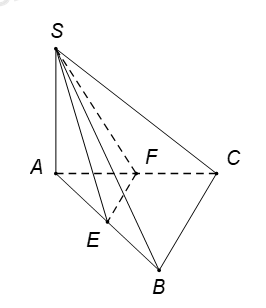
Gọi \(\left( d \right)\) là đường thẳng đi qua \(S\) và song song với EF.

Vì EF là đường trung bình tam giác ABC suy ra EF // BC.

Khi đó d // EF // BC\(\Rightarrow \left( SEF \right)\cap \left( SBC \right)=\left( d \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right).\)

Ta có \(\left\{ \begin{array}{l}SA \bot BC\,\,\,\,\left( {SA \bot \left( {ABC} \right)} \right)\\AB \bot BC\end{array} \right.\)\(\Rightarrow \)

\(BC \bot \left( {SAB} \right) \Rightarrow \left\{ \begin{array}{l}BC \bot SE\\BC \bot SB\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).\)

Từ \(\left( 1 \right),\,\,\left( 2 \right)\) suy ra \(\left\{ \begin{array}{l}\left( d \right) \bot SE\\\left( d \right) \bot SB\end{array} \right. \Rightarrow \widehat {\left( {\left( {SEF} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {SE;SB} \right)} = \widehat {BSE}.\)

Chọn C.