Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi tâm \(I\), cạnh \(a\), góc \(\widehat{BAD}={{60}^{0}}\), \(SA=SB=SD=\frac{a\sqrt{3}}{2}\). Gọi \(\varphi \) là góc giữa hai mặt phẳng \(\left( SBD \right)\) và \(\left( ABCD \right).\) Mệnh đề nào sau đây đúng?
- A
\(\tan \varphi =\sqrt{5}.\)
- B
\(\tan \varphi =\frac{\sqrt{5}}{5}.\)
- C
\(\tan \varphi =\frac{\sqrt{3}}{2}.\)
- D \(\varphi ={{45}^{0}}.\)
Phương pháp giải:
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông
Lời giải chi tiết:
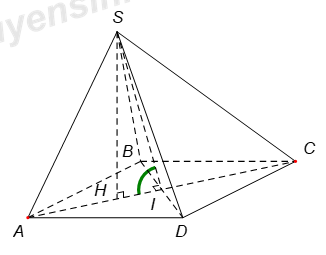
Từ giả thiết suy ra tam giác \(ABD\) đều cạnh \(a\).
Gọi \(H\) là hình chiếu của \(S\) trên mặt phẳng \(\left( ABCD \right)\).
Do \(SA=SB=SD\) nên suy ra \(H\) là tâm của tam gác đều \(ABD\).
Suy ra \(AH=\frac{2}{3}AI=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3},HI=\frac{1}{3}AI=\frac{1}{3}\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}\)
và \(SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\frac{a\sqrt{15}}{6}.\)
Vì \(ABCD\) là hình thoi nên \(HI\bot BD\). Tam giác \(SBD\) cân tại \(S\) nên \(SI\bot BD\). Do đó \(\widehat{\left( SBD \right);\left( ABCD \right)}=\widehat{\left( SI;AI \right)}=\widehat{SIH}.\).
Trong tam vuông \(SHI\), có \(\tan \widehat{SIH}=\frac{SH}{HI}=\sqrt{5}.\)
Chọn A.







