Câu hỏi
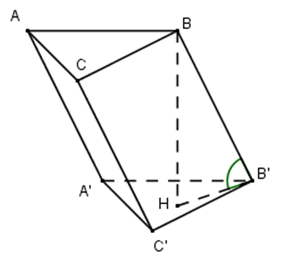
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a. Cạnh bên \(BB'=a\sqrt{3}\) và tạo với đáy một góc 300. Tính thể tích khối lăng trụ ABC.A’B’C’.
- A \(\frac{{{a}^{3}}\sqrt{3}}{8}\)
- B \(\frac{{{a}^{3}}}{8}\)
- C \(\frac{3{{a}^{3}}\sqrt{3}}{8}\)
- D \(\frac{3{{a}^{3}}}{8}\)
Phương pháp giải:
Xác định góc giữa BB’ và mặt đáy là góc giữa BB’ và hình chiếu của BB’ trên mặt đáy.
Tính \({{V}_{lt}}=Bh\), trong đó B là diện tích đáy và h là chiều cao của lăng trụ.
Lời giải chi tiết:
Gọi H là hình chiếu của B trên (A’B’C’) ta có:
\(\widehat{\left( BB';\left( A'B'C' \right) \right)}=\widehat{\left( BB';HB' \right)}=\widehat{BB'H}={{30}^{0}}\)
Xét tam giác vuông BB’H có: \(BH=BB'.\sin 30=\frac{a\sqrt{3}}{2}\)
\(\Rightarrow {{V}_{ABC.A'B'C'}}=BH.{{S}_{\Delta A'B'C'}}=\frac{a\sqrt{3}}{2}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{3{{a}^{3}}}{8}\)
Chọn D.
Câu hỏi trước
