Câu hỏi
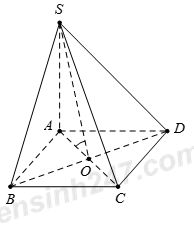
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Cạnh bên SA = 2a và vuông góc với mặt đáy (ABCD). Gọi \(\varphi \) là góc giữa SO và mặt phẳng (ABCD). Mệnh đề nào sau đây đúng?
- A \(\tan \varphi = 2\sqrt 2 .\)
- B \(\varphi = {60^0}.\)
- C \(\tan \varphi = 2.\)
- D \(\varphi = {45^0}.\)
Phương pháp giải:
Áp dụng phương pháp tìm góc giữa đường thẳng và mặt phẳng – hệ thức lượng trong tam giác vuông để giải quyết yêu cầu của bài toán
Lời giải chi tiết:
Vì \(SA \bot \left( {ABCD} \right)\) nên hình chiếu vuông góc của SO trên mặt đáy (ABCD) là AO. Do đó \(\widehat {\left( {SO;\left( {ABCD} \right)} \right)} = \widehat {\left( {SO;OA} \right)} = \widehat {SOA}.\)
Trong tam giác vuông SAO, ta có
\(\tan \widehat {SOA} = \frac{{SA}}{{OA}} = \frac{{SA}}{{\frac{1}{2}AC}} = \frac{{2a}}{{\frac{1}{2}a\sqrt 2 }} = 2\sqrt 2 .\)
Vậy đường thẳng SO hợp với mặt đáy (ABCD) một góc nhọn \(\varphi \) thỏa mãn \(\tan \varphi = 2\sqrt 2 \).
Chọn A.