Câu hỏi
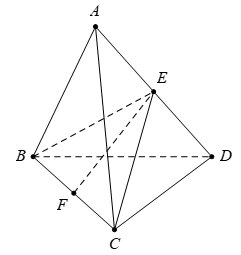
Cho tứ diện đều \(ABCD\) cạnh \(a=12,\) gọi \(\left( P \right)\) là mặt phẳng qua \(B\) và vuông góc với \(AD.\) Thiết diện của \(\left( P \right)\) và hình chóp có diện tích bằng
- A \(36\sqrt{2}.\)
- B \(40.\)
- C \(36\sqrt{3}.\)
- D \(36.\)
Phương pháp giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, cụ thể là tính diện tích
Lời giải chi tiết:
Gọi E là trung điểm của AD ta có \(BE\bot AD,CE\bot AD\Rightarrow AD\bot \left( BCE \right)\Rightarrow \left( P \right)\equiv \left( BCD \right)\)
Thiết diện là tam giác BCE.
Gọi F là trung điểm của BC.
Ta có \(BE=CE=\frac{12\sqrt{3}}{2}=6\sqrt{3};\,\,EF=\sqrt{B{{E}^{2}}-B{{F}^{2}}}=6\sqrt{2}\).
Diện tích thiết diện là \(S=\frac{1}{2}EF.BC=\frac{1}{2}.6\sqrt{2}.12=36\sqrt{2}\).
Chọn A.