Câu hỏi
Đường thẳng \(y=m\) cắt đồ thị hàm số \(y={{x}^{3}}-3x+2\) tại ba điểm phân biệt khi
- A \(0\le m<4\).
- B \(m\ge 4\).
- C \(0<m<4\).
- D \(0<m\le 4\).
Phương pháp giải:
Sử dụng đồ thị (bảng biến thiên) để tìm số giao điểm của hai đồ thị hàm số.
Lời giải chi tiết:
Ta lập BBT của hàm số \(y={{x}^{3}}-3x+2\).
Ta có \(y' = 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\).
BBT:
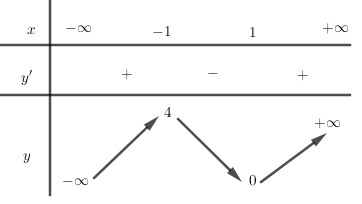
Từ BBT để đường thẳng y=m cắt đồ thị hàm số \(y={{x}^{3}}-3x+2\) tại ba điểm phân biệt thì \(0<m<4\).
Chọn C.
Câu hỏi trước
