Câu hỏi
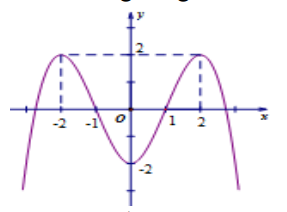
Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số sau:
- A \(y=-\frac{{{x}^{4}}}{2}+2{{x}^{2}}-2\).
- B \(y=-\frac{{{x}^{4}}}{4}+{{x}^{2}}-2\).
- C \(y=-{{\left| x \right|}^{3}}+5\left| x \right|-2\).
- D \(y=-{{\left| x \right|}^{3}}+3{{x}^{2}}-2\).
Phương pháp giải:
Sử dụng phương pháp loại trừ.
+) Xác định hình dáng đồ thị, dựa vào \(\underset{x\to \pm \infty }{\mathop{\lim }}\,y\) để xác định dấu của hệ số a.
+) Từ đồ thị hàm số ta biết được các điểm cực trị, số giao điểm với trục hoành và trục tung từ đó suy ra đáp án.
Lời giải chi tiết:
+) Từ đồ thị hàm số ta có các điểm cực trị \(\left( -2;2 \right),\left( 2;2 \right),\left( 0;-2 \right)\) và có bốn giao điểm với trục hoành trong đó có hai giao điểm là \(\left( -1;0 \right)\) và \(\left( 1;0 \right)\).
+) Xét hàm số \(y=-\frac{{{x}^{4}}}{2}+2{{x}^{2}}-2\) ta thay \(x=-1;y=0\) thấy không thỏa mãn phương trình nên loại A.
+) Xét hàm số \(y=-\frac{{{x}^{4}}}{4}+{{x}^{2}}-2\)ta thay \(x=-1;y=0\) thấy không thỏa mãn nên loại B.
+) Xét hàm số \(y=-{{\left| x \right|}^{3}}-5\left| x \right|-2\) ta thay \(x=-1;y=0\) thấy không thỏa mãn nên loại C.
+) Xét hàm số \(y=-{{\left| x \right|}^{3}}+3{{x}^{2}}-2\) ta thay các điểm \(\left( -2;2 \right),\left( 2;2 \right),\left( 0;-2 \right)\);\(\left( -1;0 \right)\);\(\left( 1;0 \right)\) thấy thỏa mãn.
Chọn D.







