Câu hỏi
Cho hình vuông ABCD tâm O, cạnh bằng 2a. Trên đường thẳng qua O và vuông góc với mặt phẳng (ABCD) lấy điểm S. Biết góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng \({{45}^{0}}.\) Độ dài cạnh SO bằng :
- A \(SO=a\sqrt{3}.\)
- B \(SO=a\sqrt{2}.\)
- C \(SO=\frac{a\sqrt{3}}{2}.\)
- D \(SO=\frac{a\sqrt{2}}{2}.\)
Phương pháp giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng để xác định góc giữa đường thẳng và mặt phẳng
Lời giải chi tiết:
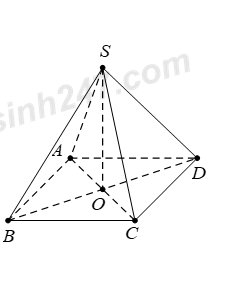
Vì O là hình chiếu của S trên mặt phẳng (ABCD).
Suy ra OA là hình chiếu của SA trên mặt phẳng (ABCD)
\(\Rightarrow \widehat{SA;\left( ABCD \right)}=\widehat{\left( SA;OA \right)}=\widehat{SAO}={{45}^{0}}\,\,\Rightarrow \,\,\Delta SAO\) vuông cân tại O (1)
Tam giác ABC vuông cân tại B, có \(OA=\frac{AC}{2}=\frac{AB\sqrt{2}}{2}=a\sqrt{2}.\) \(\left( 2 \right)\)
Từ (1), (2) suy ra \(SO=OA=a\sqrt{2}.\)
Chọn B.







