Câu hỏi
Cho hình chóp S.ABC có đáy ABC là tam giác nhọn, cạnh bên SA = SB = SC. Gọi H là hình chiếu vuông góc của S trên mặt phẳng (ABC), khi đó
- A H là trực tâm của tam giác ABC
- B H là trọng tâm của tam giác ABC.
- C H là tâm đường tròn ngoại tiếp tam giác ABC
- D H là tâm đường tròn nội tiếp tam giác ABC.
Phương pháp giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng
Lời giải chi tiết:
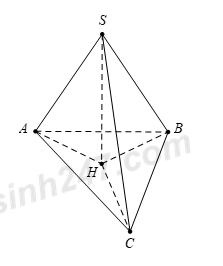
Vì H là hình chiếu vuông góc của S trên mp(ABC) nên ta có
Tam giác SAH vuông tại H, có \(S{{A}^{2}}=A{{H}^{2}}+S{{H}^{2}}.\)
Tam giác SBH vuông tại H, có \(S{{B}^{2}}=B{{H}^{2}}+S{{H}^{2}}.\)
Tam giác SCH vuông tại H, có \(S{{C}^{2}}=C{{H}^{2}}+S{{H}^{2}}.\)
Kết hợp điều kiện \(SA=SB=SC\)suy ra \(HA=HB=HC\) nên \(H\) là tâm
đường tròn ngoại tiếp tam giác \(ABC.\)
Chọn C.
Câu hỏi trước
