Câu hỏi
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O. Đường thẳng SA vuông góc với mặt đáy (ABCD). Gọi I là trung điểm của SC. Khẳng định nào dưới đây là sai ?
- A \(IO\bot \left( ABCD \right).\)
- B \(BC\bot SB.\)
- C Tam giác SCD vuông ở D.
- D (SAC) là mặt phẳng trung trực của BD.
Phương pháp giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng
Lời giải chi tiết:
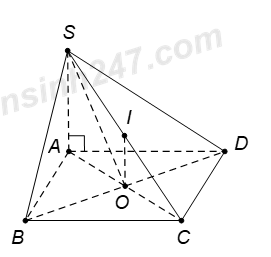
Vì \(O,\,\,I\) lần lượt là trung điểm của \(AC,\,\,SC\) suy ra \(OI\) là đường trung bình của tam giác \(SAC\)\(\Rightarrow \)\(OI\)//\(SA\) mà \(SA\bot \left( ABCD \right)\Rightarrow OI\bot \left( ABCD \right).\)
Ta có \(ABCD\) là hình chữ nhật \(\Rightarrow \,\,\,BC\bot AB\) mà \(SA\bot BC\) suy ra \(BC\bot \left( SAB \right)\Rightarrow BC\bot SB.\)
Tương tự, ta có được
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\,\,\,\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD \Rightarrow \Delta SCD\) vuông tại D.Nếu \(\left( SAC \right)\) là mặt phẳng trung trực của \(BD\,\Rightarrow BD\bot \left( SAC \right)\Rightarrow BD\bot AC\): điều này chưa chắc có thể xảy ra vì ABCD là hình chữ nhật.
Chọn D







