Câu hỏi
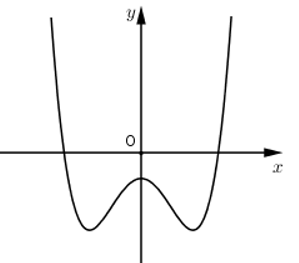
Từ đồ thị hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\left( a\ne 0 \right)\) được cho dạng như hình vẽ, ta có:
- A \(a>0,b<0,c<0\)
- B \(a>0,b>0,c<0\)
- C \(a<0,b>0,c<0\)
- D \(a>0,b<0,c>0\)
Phương pháp giải:
+) Dựa vào \(\underset{x\to -\infty }{\mathop{\lim }}\,y=+\infty \Rightarrow \) Dấu của a
+) Dựa vào giao điểm của đồ thị hàm số với trục tung \(\Rightarrow \) dấu của c.
+) Dựa vào số điểm cực trị của đồ thị hàm số \(\Rightarrow \) dấu của b.
Lời giải chi tiết:
\(\underset{x\to -\infty }{\mathop{\lim }}\,y=+\infty \Rightarrow a>0\)
Giao điểm của đồ thị hàm số với trục tung là \(\left( 0;c \right)\Rightarrow c<0\)
Ta có \(y'=4a{{x}^{3}}+2bx=0\Leftrightarrow \left[ \begin{align} & x=0 \\ & {{x}^{2}}=-\frac{b}{2a} \\ \end{align} \right.\)
Đồ thị hàm số có 3 cực trị \(\Rightarrow -\frac{b}{2a}>0\). Mà \(a>0\Rightarrow b<0\)
Chọn A.
Câu hỏi trước
