Câu hỏi
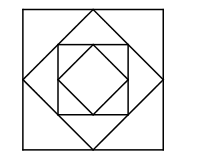
Hình vuông có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp để tạo thành một hình vuông, tiếp tục làm như vậy đối với các hình vuông mới (như hình bên). Tổng diện tích các hình vuông liên tiếp đó bằng
- A \(8\)
- B \(2\)
- C \(12\)
- D \(\dfrac{3}{2}\)
Phương pháp giải:
Lập hàm số tổng diện tích các hình vuông nhờ công thức tổng của cấp số nhân \({S_n} = \dfrac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\)
Sử dụng MTCT tính \(\lim {S_n}\)
Lời giải chi tiết:
Gọi \({S_1}\) là diện tích hình vuông cạnh 1 ban đầu ta có \({S_1} = {1^2}\)
Sau khi nối các trung điểm của hình vuông ban đầu với nhau ta được hình vuông mới có cạnh \(\dfrac{{\sqrt 2 }}{2}\) \( \Rightarrow {S_2} = {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^2} = \dfrac{1}{2}\)
Tương tự như vậy ta có \({S_3} = {\left( {\dfrac{{\sqrt 2 }}{2}.\dfrac{{\sqrt 2 }}{2}} \right)^2} = {\left( {{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}} \right)^2} = {\left( {\dfrac{1}{2}} \right)^2}\)
\({S_4} = {\left( {{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}} \right)^3} = {\left( {\dfrac{1}{2}} \right)^3};\,\,\,....\,\,;\,\,\,{S_n} = {\left( {\dfrac{1}{2}} \right)^{n - 1}}\)
Ta có tổng diện tích các hình vuông là tổng của 1 CSC có \({u_1} = 1\) và công bội \(q = \dfrac{1}{2}\)
\( \Rightarrow {S_1} + {S_2} + ... + {S_n} = \dfrac{{1\left( {1 - {{\left( {\dfrac{1}{2}} \right)}^{n - 1}}} \right)}}{{1 - \dfrac{1}{2}}}\), ta tính giới hạn \(\lim \dfrac{{1\left( {1 - {{\left( {\dfrac{1}{2}} \right)}^{n - 1}}} \right)}}{{1 - \dfrac{1}{2}}}\) khi \(n \to + \infty \)
Nhập vào MTCT, ấn phím [CALC], chọn \(x = {10^{10}}\) ta được kết quả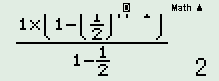
Chọn B.







