Câu hỏi
Giá trị của \(\mathop {\lim }\limits_{x \to - 1} \dfrac{{{x^2} + 1}}{{\left( {{x^2} + x} \right)\left( {{x^3} + 1} \right)}}\) bằng:
- A \( - \infty \)
- B \( + \infty \)
- C \(2\)
- D \(0\)
Phương pháp giải:
Suử dụng MTCT
Lời giải chi tiết:
Nhập \(\dfrac{{{x^2} + 1}}{{\left( {{x^2} + x} \right)\left( {{x^3} + 1} \right)}}\) vào MTCT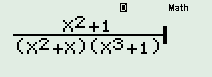
Nhấn phím [CALC], chọn \(x = - 1 + 0,000001\) ta được kết quả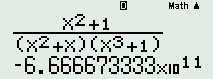
\(\mathop {\lim }\limits_{x \to - {1^ + }} \dfrac{{{x^2} + 1}}{{\left( {{x^2} + x} \right)\left( {{x^3} + 1} \right)}} = - \infty \)
Nhấn phím [CALC], chọn \(x = - 1 - 0,000001\) ta được kết quả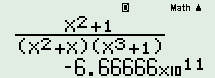
\(\mathop {\lim }\limits_{x \to - {1^ - }} \dfrac{{{x^2} + 1}}{{\left( {{x^2} + x} \right)\left( {{x^3} + 1} \right)}} = - \infty \)
Vậy \(\mathop {\lim }\limits_{x \to - 1} \dfrac{{{x^2} + 1}}{{\left( {{x^2} + x} \right)\left( {{x^3} + 1} \right)}} = - \infty \)
Chọn A.
Câu hỏi trước
