Phương pháp giải:

Dựa vào đồ thị hàm số ta dự đoán được dạng của đồ thị hàm số, sau đó dựa vào các điểm cực trị, các giao điểm của đồ thị với trục tung, trục hoành để ta tìm ra hàm số.

Lời giải chi tiết:

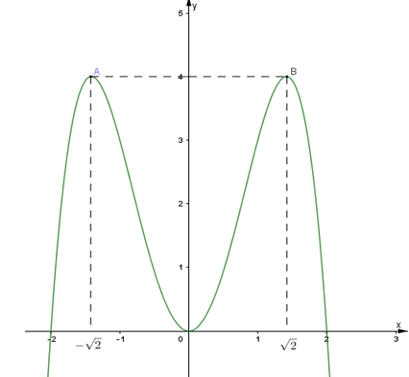
Ta thấy nét cuối của đồ thị hàm số đi xuống nên hệ số a < 0

Dựa vào hình vẽ ta có dạng của đồ thị hàm số là: \(y = a{x^4} + b{x^2} + c\,\,\left( {a \ne 0} \right)\)

Đồ thị giao với trục hoành tại điểm (0;0); (-2;0); (2;0) nên ta có: c = 0 và \(16a+4b=0\Leftrightarrow 4a+b=0\left( 1 \right)\)

Đến đây, cách tính nhanh là ta có thể thử các trường hợp B, C, D với máy tính, và thấy đáp án D thỏa mãn.

Cách tự luận:

Đồ thị hàm số đi qua 2 điểm \(\left( -\sqrt{2};4 \right);\left( \sqrt{2};4 \right)\) nên ta có: \(a.{{\left( \sqrt{2} \right)}^{4}}+b{{\left( \sqrt{2} \right)}^{2}}=4\Leftrightarrow 4a+2b=4\Leftrightarrow 2a+b=2\left( 2 \right)\)

Từ (1) và (2) ta có: 

\(\left\{ \begin{array}{l}4a + b = 0\\2a + b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = 4\end{array} \right.\)

Chọn D.