Phương pháp giải:

Bước 1: Tính đạo hàm y’.

Bước 2: Giải phương trình y’ = 0 và xét dấu của đạo hàm.

Bước 3: Kết luận hàm số đồng biến và nghịch biến

Lời giải chi tiết:

\(y=f\left( x \right)={{x}^{3}}-3{{x}^{2}}-2\Rightarrow y'=3{{x}^{2}}-6x;y'=0\Leftrightarrow 3x\left( x-2 \right)=0\Leftrightarrow \left[ \begin{align}  & x=0 \\  & x=2 \\ \end{align} \right.\)

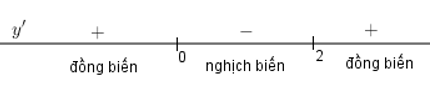
Xét dấu của y’:

Từ đó ta tìm được Hàm số f(x) nghịch biến trên khoảng \(\left( 0;2 \right)\) .

Hàm số f(x) đồng biến trên khoảng \(\left( 2;+\infty  \right)\)

Hàm số f(x) đồng biến trên khoảng \(\left( -\infty ;0 \right)\)

Chọn D.