Câu hỏi
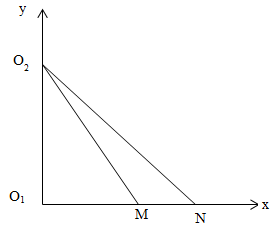
Trong một thí nghiệm về giao thoa sóng nước, hai nguồn kết hợp O1 và O2 dao động cùng pha cùng biên độ. Chọn hệ tọa độ Oxy với gốc tọa độ là vị trí đặt tại nguồn O1 còn nguồn O2 nằm trên trục Oy. Hai điểm M và N di động trên trục Ox thỏa mãn OM = a; ON = b ( a < b). Biết rằng ab = 324 cm2 ; O1O2 = 18 cm và b thuộc đoan [21,6;24] cm. Khi góc quét MO2N có giá trị lớn nhất thì thấy rằng M và N dao động với biên độ cực đại và giữa chúng có hai cực tiểu. Hỏi có bao nhiêu điểm dao động với biên độ cực đại trên đoạn nối hai nguồn
- A 22
- B 25
- C 23
- D 21
Phương pháp giải:
Sử dụng lí thuyết để có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha
Điều kiện để có cực đại giao thoa: d2 – d1 = kλ
Công thức tính số cực đại giao thoa trên đoạn thẳng nối hai nguồn: \( - {{AB} \over \lambda } < k < {{AB} \over \lambda }\)
Lời giải chi tiết:
Ta có:
\(\eqalign{ & \tan {O_1}{O_2}M = {a \over {18}};\tan {O_1}{O_2}N = {b \over {18}};ab = 324c{m^2} \cr & \tan M{O_2}N = \tan ({O_1}{O_2}N - {O_1}{O_2}M) = {{{a \over {18}} - {b \over {18}}} \over {1 + {a \over {18}}.{b \over {18}}}} = {b \over 9} - {a \over 9} \cr} \)
Để góc MO2N lớn nhất thì bmax và amin
Mà:
\(\left\{ \matrix{ b \in \left[ {21,6;{\rm{ }}24} \right]{\rm{ }}cm \hfill \cr ab = 324c{m^2} \hfill \cr} \right. \Rightarrow \left\{ \matrix{ {b_{m{\rm{ax}}}} = 24cm = {O_1}N \hfill \cr {a_{\min }} = 13,5cm = {O_1}M \hfill \cr} \right.\)
Áp dụng định lí Pi – ta – go trong tam giác vuông O1O2M và O1O2N ta tính được: O2M = 22,5cm; O2N = 30cm
Điều kiện để có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha: d2 – d1 = kλ
Giả sử M thuộc cực đại bậc k. Do giữa M và N có hai cực tiểu => N thuộc cực đại bậc k – 2
\( \Rightarrow \left\{ \matrix{ {O_2}M - {O_1}M = k\lambda \hfill \cr {O_2}N - {O_1}N = (k - 2)\lambda \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ 22,5 - 13,5 = k\lambda \hfill \cr 30 - 24 = (k - 2)\lambda \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ 9 = k\lambda \hfill \cr 6 = (k - 2)\lambda \hfill \cr} \right. \Rightarrow \lambda = 1,5cm\)
Số cực đại trên đoạn thẳng hai nguồn bằng số giá trị k nguyên thoả mãn:
\( - {{{O_1}{O_2}} \over \lambda } < k < {{{O_1}{O_2}} \over \lambda } \Leftrightarrow - {{18} \over {1,5}} < k < {{18} \over {1,5}} \Leftrightarrow - 12 < k < 12 \Rightarrow k = - 11; - 10;...;11\)
Có 23 giá trị của k nguyên => có 23 điểm dao động với biên độ cực đại trên đoạn thẳng nối hai nguồn
Chọn C