Phương pháp giải:

Xác định thiết diện của mp(α).

Dựa vào định lí Simson tính tỉ lệ thể tích các khối chóp tam giác \(\dfrac{{{V_{S.{A_1}{B_1}{C_1}}}}}{{{V_{S.ABC}}}} = \dfrac{{S{A_1}}}{{SA}}.\dfrac{{S{B_1}}}{{SB}}.\dfrac{{S{C_1}}}{{SC}}\), với \({A_1} \in SA,{B_1} \in SB,{C_1} \in SC\).

Lời giải chi tiết:

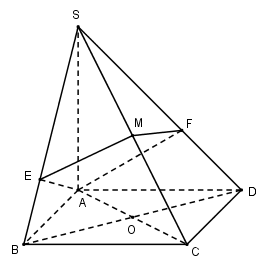
Xét tam giác vuông ABC có \(AC = \sqrt {{a^2} + 3{a^2}}  = 2a = SA \Rightarrow \Delta SAC\) vuông cân tại A \(\Rightarrow AM \bot SC \Rightarrow AM \subset \left( \alpha  \right)\)

Trong mp(SAB) kẻ \(AE \bot SB\) ta có:  

\(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AE \Rightarrow AE \bot \left( {SBC} \right) \Rightarrow AE \bot SC \Rightarrow AE \subset \left( \alpha \right)\)

Trong mp(SAD) kẻ \(AF \bot SD\) ta có:

\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AF \Rightarrow AF \bot \left( {SCD} \right) \Rightarrow AF \bot SC \Rightarrow AF \subset \left( \alpha \right)\)

Do đó mp(α) chính là mp(AEMF).

Xét tam giác vuông SAB có \(\dfrac{{SE}}{{SB}} = \dfrac{{S{A^2}}}{{S{B^2}}} = \dfrac{{S{A^2}}}{{S{A^2} + A{B^2}}} = \dfrac{{4{a^2}}}{{4{a^2} + {a^2}}} = \dfrac{4}{5}\)

Xét tam giác vuông SAD có \(\dfrac{{SF}}{{SD}} = \dfrac{{S{A^2}}}{{S{D^2}}} = \dfrac{{S{A^2}}}{{S{A^2} + A{D^2}}} = \dfrac{{4{a^2}}}{{4{a^2} + 3{a^2}}} = \dfrac{4}{7}\)

Ta có:

\(\begin{array}{l}\dfrac{{{V_{S.AEM}}}}{{{V_{S.ABC}}}} = \dfrac{{SE}}{{SB}}.\dfrac{{SM}}{{SC}} = \dfrac{4}{5}.\dfrac{1}{2} = \dfrac{2}{5} \Rightarrow {V_{S.AEM}} = \dfrac{2}{5}{V_{S.ABC}} = \dfrac{2}{5}.\dfrac{1}{2}{V_{S.ABCD}} = \dfrac{1}{5}{V_{S.ABCD}}\\\dfrac{{{V_{S.AMF}}}}{{{V_{S.ACD}}}} = \dfrac{{SM}}{{SC}}.\dfrac{{SF}}{{SD}} = \dfrac{1}{2}.\dfrac{4}{7} = \dfrac{2}{7} \Rightarrow {V_{S.AMF}} = \dfrac{2}{7}{V_{S.ABC}} = \dfrac{2}{7}.\dfrac{1}{2}{V_{S.ABCD}} = \dfrac{1}{7}{V_{S.ABCD}}\\ \Rightarrow {V_{S.AEMF}} = {V_{S.AEM}} + {V_{S.AMF}} = \dfrac{{12}}{{35}}{V_{S.ABCD}}\end{array}\)

Gọi thể tích khối đa diện không chứa S là V thì \(V = \dfrac{{23}}{{35}}{V_{S.ABCD}}\)

Ta có \({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}SA.AB.AD = \dfrac{1}{3}.2a.a.a\sqrt 3  = \dfrac{{2\sqrt 3 {a^3}}}{3}\)

\( \Rightarrow V = \dfrac{{23}}{{35}}{V_{S.ABCD}} = \dfrac{{23}}{{35}}.\dfrac{{2\sqrt 3 {a^3}}}{3} = \dfrac{{46\sqrt 3 {a^3}}}{{105}}\)

Chọn A