 Môn Toán - Lớp 12
Môn Toán - Lớp 12
 40 bài tập trắc nghiệm sự đồng biến nghịch biến của hàm số mức độ vận dụng, vận dụng cao
40 bài tập trắc nghiệm sự đồng biến nghịch biến của hàm số mức độ vận dụng, vận dụng cao
Câu hỏi
Tìm tất cả các giá trị thực của m để hàm số \(y = \dfrac{1}{3}{x^3} - 2{x^2} + \left( {m + 5} \right)x + 2m - 5\) đồng biến trên khoảng \(\left( {3; + \infty } \right)\)
- A \(m \le 2\)
- B \(m > - 2\)
- C \(m < 2\)
- D \(m \ge - 2\)
Phương pháp giải:
Áp dụng lý thuyết về tính đồng biến của hàm số
Lời giải chi tiết:
Ta có: \(y = \dfrac{1}{3}{x^3} - 2{x^2} + \left( {m + 5} \right)x + 2m - 5 \Rightarrow y' = {x^2} - 4x + m + 5\) với \(\Delta {'_{y'}} = - m - 1\)
- Nếu \(m \ge - 1 \Rightarrow - m - 1 \le 0 \Rightarrow \Delta {'_{y'}} \le 0 \Rightarrow y' \ge 0\forall x\)
Khi đó hàm số đồng biến trên R hay hàm số đồng biến trên khoảng \(\left( {3; + \infty } \right)\)
- Nếu \(m < - 1 \Rightarrow - m - 1 > 0 \Rightarrow \Delta {'_{y'}} > 0\). Khi đó phương trình \(y' = 0\) có hai nghiệm phân biệt \({x_1};{x_2}\left( {{x_1} < {x_2}} \right)\)
Ta có bảng biến thiên của y:
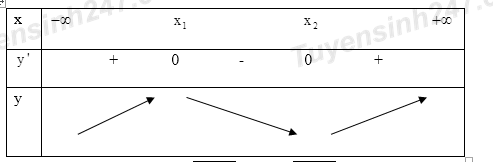
Hàm số đồng biến trên \(\left( {3; + \infty } \right) \Leftrightarrow {x_2} \le 3 \Leftrightarrow 2 + \sqrt { - m - 1} \le 3 \Leftrightarrow \sqrt { - m - 1} \le 1 \Leftrightarrow 0 \le - m - 1 \le 1 \Leftrightarrow - 2 \le m \le - 1\)
Kết hợp nghiệm ta có \(m \in \left[ { - 2; - 1} \right] \cup \left[ { - 1; + \infty } \right) = \left[ { - 2; + \infty } \right)\) hay \(m \ge - 2\).
Chọn D.






