Câu hỏi
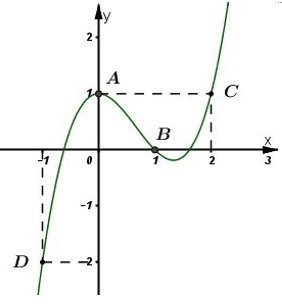
Cho hàm số \(y=f\left( x \right)\) với đạo hàm \({f}'\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(g\left( x \right)=f\left( x \right)-\frac{{{x}^{3}}}{3}+{{x}^{2}}-x+2\) đạt cực đại tại điểm nào ?
- A \(x=-\,1.\)
- B \(x=1.\)
- C \(x=0.\)
- D \(x=2.\)
Phương pháp giải:
Dựa vào bảng biến thiên của hàm số để kết luận điểm cực trị
Lời giải chi tiết:
Lời giải:
Xét hàm số \(g\left( x \right)=f\left( x \right)-\frac{{{x}^{3}}}{3}+{{x}^{2}}-x+2,\) có \({g}'\left( x \right)={f}'\left( x \right)-{{x}^{2}}+2x-1;\,\,\forall x\in R\)
Ta có \({g}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)={{\left( x-1 \right)}^{2}}\,\,\,\,\,\,\,\,\,\left( * \right)\)
Từ đồ thị hàm số \(f'\left( x \right)\) ta thấy: \(f'\left( 0 \right)=1={{\left( 0-1 \right)}^{2}}\) nên \(x=0\) là một nghiệm của \(g'\left( x \right)\).
\(f'\left( 1 \right)=0={{\left( 1-1 \right)}^{2}}\Rightarrow x=1\) là một nghiệm của \(g'\left( x \right)\).
\(f'\left( 2 \right)=1={{\left( 2-1 \right)}^{2}}\Rightarrow x=2\) là một nghiệm của \(g'\left( x \right)\).
Vậy phương trình \(\left( * \right)\) có ba nghiệm phân biệt \({{x}_{1}}=0,\,\,{{x}_{2}}=1,\,\,{{x}_{3}}=2.\)
Vẽ đồ thị hàm số \(y={{\left( x-1 \right)}^{2}}\) trên cùng mặt phẳng tọa độ với \(y=f'\left( x \right)\) ta thấy:
Trong khoảng \(\left( 0;1 \right)\) thì đồ thị hàm số \(y=f'\left( x \right)\) nằm phía trên đồ thị hàm số \(y={{\left( x-1 \right)}^{2}}\) nên \(g'\left( x \right)>0,\forall x\in \left( 0;1 \right)\).
Trong khoảng \(\left( 1;2 \right)\) thì đồ thị hàm số \(y=f'\left( x \right)\) nằm phía dưới đồ thị hàm số \(y={{\left( x-1 \right)}^{2}}\) nên \(g'\left( x \right)<0,\forall x\in \left( 1;2 \right)\).
Vậy \(x=1\) là điểm cực đại của hàm số \(y=g\left( x \right).\)
Chọn B