Câu hỏi
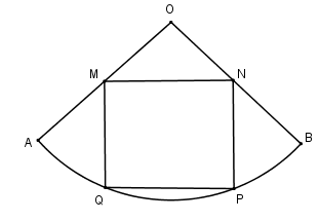
Cho tấm tôn hình nón có bán kính đáy là \(r=\frac{2}{3}\), độ dài đường sinh l = 2. Người ta cắt theo một đường sinh và trải phẳng ra được một hình quạt. Gọi M, N thứ tự là trung điểm OA và OB. Hỏi khi cắt hình quạt theo hình chữ nhật MNPQ (hình vẽ) và tạo thành hình trụ đường sinh PN trùng MQ (2 đáy làm riêng) thì được khối trụ có thể tích bằng bao nhiêu?
- A \(\frac{3\pi \left( \sqrt{13}-1 \right)}{8}\)
- B \(\frac{3\left( \sqrt{13}-1 \right)}{4\pi }\)
- C \(\frac{5\left( \sqrt{13}-1 \right)}{12\pi }\)
- D \(\frac{\pi \left( \sqrt{13}-1 \right)}{9}\)
Phương pháp giải:
Tính độ dài các đoạn thẳng MN và MQ sau đó áp dụng công thức tình thể tích hình trụ \(V=\pi {{r}^{2}}h\) .
Lời giải chi tiết:
Cách giải:
Độ dài cung AB là chu vi đường tròn đáy nên \({{l}_{\overset\frown{AB}}}=2\pi .r=2\pi \frac{2}{3}=\frac{4\pi }{3}\)
Ta có độ dài cung AB là \({{l}_{\overset\frown{AB}}}=\alpha .OA\Rightarrow \alpha =\frac{{{l}_{\overset\frown{AB}}}}{OA}=\frac{\frac{4\pi }{3}}{2}=\frac{2\pi }{3}=\widehat{AOB}\)
Áp dụng định lí cosin trong tam giác OAB có \(\begin{align} & AB=\sqrt{O{{A}^{2}}+O{{B}^{2}}-2OA.OB.\cos \frac{2\pi }{3}}=\sqrt{{{2}^{2}}+{{2}^{2}}-{{2.2}^{2}}\left( -\frac{1}{2} \right)}=2\sqrt{3} \\ & MN=\frac{1}{2}AB=\sqrt{3}=PQ\Rightarrow MH=\frac{1}{2}MN=\frac{\sqrt{3}}{2} \\ \end{align}\)
Hạ \(OD\bot MN\) ta có OD là tia phân giác của \(\widehat{AOB}\Rightarrow \widehat{AOD}={{60}^{0}}\), OD cắt AQ tại E.
Xét tam giác vuông OMH có \(OH=OM.\cos 60=1.\frac{1}{2}=\frac{1}{2}\)
Xét tam giác OPQ có \(\cos \widehat{POQ}=\frac{O{{P}^{2}}+O{{Q}^{2}}-P{{Q}^{2}}}{2.OP.OQ}=\frac{4+4-3}{2.2.2}=\frac{5}{8}\)
Mà \(\cos \widehat{POQ}=\cos \left( 2\widehat{DOQ} \right)=2{{\cos }^{2}}\widehat{DOQ}-1=\frac{5}{8}\Leftrightarrow \cos \widehat{DOQ}=\frac{\sqrt{13}}{4}\)
Xét tam giác DOQ có \(Q{{D}^{2}}=O{{Q}^{2}}+O{{D}^{2}}-2OQ.OD\cos \widehat{DOQ}=4+4-2.2.2.\frac{\sqrt{13}}{4}=8-2\sqrt{13}\)
Xét tam giác vuông DQF có : \(D{{F}^{2}}=Q{{D}^{2}}-Q{{F}^{2}}=8-2\sqrt{13}-\frac{3}{4}=\frac{29}{4}-2\sqrt{13}\Leftrightarrow DF=\frac{\sqrt{29-8\sqrt{13}}}{2}=\frac{\sqrt{16-2.4.\sqrt{13}+13}}{2}=\frac{4-\sqrt{13}}{2}\)
\(\Rightarrow HF=OD-OH-DF=2-\frac{1}{2}-\frac{4-\sqrt{13}}{2}=\frac{4-1-4+\sqrt{13}}{2}=\frac{\sqrt{13}-1}{2}=MQ\)
Khi đó thể tích khối trụ tạo ra bởi hình chữ nhật MNPQ là
\(V=\pi .M{{H}^{2}}.MQ=\pi .{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}.\frac{\sqrt{13}-1}{2}=\frac{3\pi \left( \sqrt{13}-1 \right)}{8}\).
Chọn A.