Câu hỏi
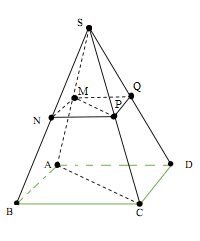
Cho hình chóp tứ giác \(S.ABC{\rm{D}}\)có \(M,N,P,Q\) lần lượt là trung điểm của các cạnh \(SA,SB,SC,S{\rm{D}}\). Tỉ số \(\frac{{{V_{S.MNPQ}}}}{{{V_{S.ABC{\rm{D}}}}}}\) là
- A \(\frac{1}{8}\)
- B \(\frac{1}{{16}}\)
- C \(\frac{3}{8}\)
- D \(\frac{1}{6}\)
Phương pháp giải:
Áp dụng công thức tỉ lệ thể tích trong khối chóp tam giác:
Mặt phẳng \(\left( P \right)\) cắt ba mặt bên của khối chóp tam giác theo thiết diện là tam giác \(A'B'C'\) với \(A' \in SA,B' \in SB,C' \in SC\). Khi đó: \(\frac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \frac{{SA'}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}}\).
Lời giải chi tiết:
Theo công thức tỉ lệ tứ diện ta có
\(\frac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}}.\frac{{SP}}{{SC}} = \frac{1}{8}\)
\(\frac{{{V_{S.MPQ}}}}{{{V_{S.AC{\rm{D}}}}}} = \frac{{SM}}{{SA}}.\frac{{SP}}{{SC}}.\frac{{SQ}}{{SD}} = \frac{1}{8}\)
Theo dãy tỉ số bằng nhau ta có
\(\frac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \frac{{{V_{S.MPQ}}}}{{{V_{S.AC{\rm{D}}}}}} = \frac{{{V_{S.MPQ}} + {V_{S.MNP}}}}{{{V_{S.AC{\rm{D}}}} + {V_{S.ABC}}}} = \frac{{{V_{S.MNPQ}}}}{{{V_{S.ABCD}}}} = \frac{1}{8}\)