Câu hỏi
Tìm các giá trị của tham số \(m\) để phương trình: \({x^3} - 3x = {m^2} + m\) có 3 nghiệm phân biệt?
- A \( - 2 < m < 1\)
- B \( - 1 < m < 2\)
- C \(m < 1\)
- D \(m > - 21\)
Phương pháp giải:
Khảo sát hàm số \(y = {x^3} - 3x\), sự dụng sự tương giao đồ thị để tìm điều kiện của \(m\).
Lời giải chi tiết:
Ta có: \(y' = 3{{\rm{x}}^2} - 3\)
\( \Rightarrow y' = 0 \Leftrightarrow x = - 1\) hoặc \(x = 1\)
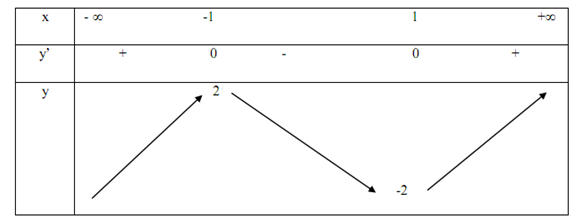
Ta có bảng biến thiên
Từ bảng biến thiên, phương trình có 3 nghiệm phân biệt
\( \Leftrightarrow - 2 < {m^2} + m < 2 \Leftrightarrow \left\{\begin{array}{l}{m^2} + m + 2 > 0\\{m^2} + m - 2 < 0\end{array} \right. \Leftrightarrow {m^2} + m - 2 < 0 \Leftrightarrow - 2 < m < 1\)