Phương pháp giải:

Lập bảng biến thiên cho hàm số \(y = {x^4} - 2{x^2}\), từ đó suy ra bảng biến thiên của hàm số \(y = \left| {{x^4} - 2{x^2}} \right|\).

Phương trình đã cho có \(6\) nghiệm thực phân biệt khi và chỉ khi đường thẳng \(y = m\) cắt đồ thị hàm số \(y = \left| {{x^4} - 2{x^2}} \right|\) tại \(6\) điểm phân biệt.

Lời giải chi tiết:

Xét hàm số \(y = {x^4} - 2{{\rm{x}}^2}\)

Ta có: \(y' = 4{{\rm{x}}^3} - 4{\rm{x}}\)

\( \Rightarrow y = 0 \Leftrightarrow x = 0\) hoặc \(x = 1\) hoặc \(x =  - 1\)

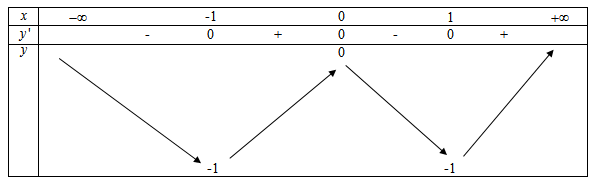
Ta có bảng biến thiên

Từ bảng biến thiên hàm số \(y = {x^4} - 2{{\rm{x}}^2}\) ta thấy đường thẳng \(y = 0\) cắt đồ thị hàm số \(y = {x^4} - 2{x^2}\) tại ba điểm có hoành độ \(x = 0;x =  \pm \sqrt 2 \)

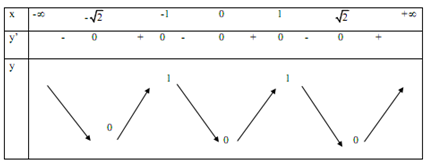
Ta có bảng biến thiên hàm \(y = \left| {{x^4} - 2{{\rm{x}}^2}} \right|\) có được từ bảng biến thiên của hàm số \(y = {x^4} - 2{x^2}\) như sau: (có được từ việc lấy đối xứng phần giá trị của hàm số mà nhỏ hơn 0 qua trục Ox)

Vậy phương trình \({x^2}\left| {{x^2} - 2} \right| = m\) có 6 nghiệm khi \(0 < m < 1\)