Câu hỏi
Hàm số \(y = - {x^4} - 2{x^2} + 3\) nghịch biến trên
- A \(\left( { - \infty ;0} \right)\)
- B \(\left( { - \infty ; - 1} \right)\)và \(\left( {0;1} \right)\)
- C Tập số thực \(R\)
- D \(\left( {0; + \infty } \right)\)
Phương pháp giải:
Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {a;b} \right)\) nếu \(f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)\).
Lời giải chi tiết:
Ta có: \(y' = - 4{x^3} - 4{\rm{x}}\)\( \Rightarrow y' = 0 \Leftrightarrow x = 0\)
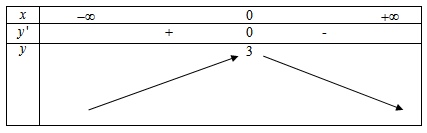
Ta có bảng biến thiên
Từ bảng biến thiên ta thấy hàm nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)
Câu hỏi trước
