Câu hỏi
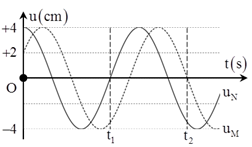
Sóng ngang có tần số f truyền trên một sợi dây đàn hồi rất dài, với tốc độ 3 m/s. Xét hai điểm M và N nằm trên cùng một phương truyền sóng, cách nhau một khoảng x. Đồ thị biểu diễn li độ sóng của M và N cùng theo thời gian t như hình vẽ. Biết t1 = 0,05 s. Tại thời điểm t2, khoảng cách giữa hai phần tử chất lỏng tại M và N có giá trị gần giá trị nào nhất sau đây?
- A 4,8 cm.
- B 6,7 cm.
- C 3,3 cm.
- D 3,5 cm
Phương pháp giải:
Phương pháp: Độ lệch pha của hai phần tử trên phương truyền sóng
Lời giải chi tiết:
Đáp án A
Phương trình dao động của hai phần tử M, N là
$$\left\{ \matrix{ {u_N} = 4\cos (\omega t) \hfill \cr {u_M} = 4\cos (\omega t - {\pi \over 3}) \hfill \cr} \right.cm$$
Ta thấy rằng khoảng thời gian $$\Delta {t_1} = {3 \over 4}T = 0,05 = > T = {1 \over {15}}s = > \omega = 30\pi \,rad/s$$
Độ lệch pha giữa hai sóng :$$\Delta \varphi = {\pi \over 3} = {{2\pi x} \over \lambda } = > x = {\lambda \over 6} = {{vT} \over 6} = {{10} \over 3}cm$$
Thời điểm $${t_2} = T + {5 \over {12}}T = {{17} \over {180}}s$$ khi đó điểm M đang có li độ bằng 0 và li độ của điểm N là
$${u_N} = 4\cos \omega t = 4\cos \left( {30\pi {{17} \over {180}}} \right) = - 2\sqrt 3 cm$$
Khoảng cách giữa hai phần tử MN : $$d = \sqrt {{x^2} + \Delta {u^2}} = \sqrt {{{\left( {{{10} \over 3}} \right)}^2} + {{\left( { - 2\sqrt 3 } \right)}^2}} = {{4\sqrt {13} } \over 3}cm$$