Câu hỏi
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(R\) đồng thời hàm số \(y = \left| {f\left( x \right)} \right|\) có đồ thị như hình vẽ bên
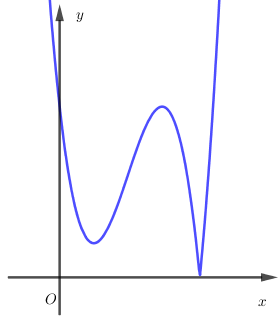
Xác định số cực trị của hàm số \(y = f\left( {\left| x \right|} \right)\)
- A \(2\)
- B \(3\)
- C \(4\)
- D \(5\)
Phương pháp giải:
- Dựng đồ thị hàm số \(y = f\left( x \right)\) từ đồ thị hàm số \)y = \left| {f\left( x \right)} \right|\):
- Dựng đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) có được từ đồ thị hàm số \(f\left( x \right)\).
Lời giải chi tiết:
Từ hình vẽ ta có đồ thị hàm số \(y = f\left( x \right)\) là một trong hai đồ thị dưới đây:
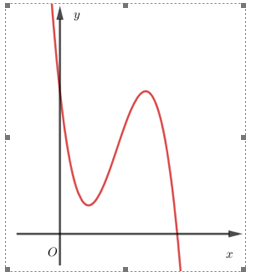
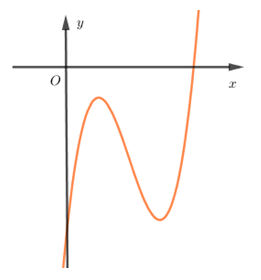
Từ hai đồ thị trên ta dựng được đồ thị \)y = f\left( {\left| x \right|} \right)\) là một trong đồ thị dưới đây:
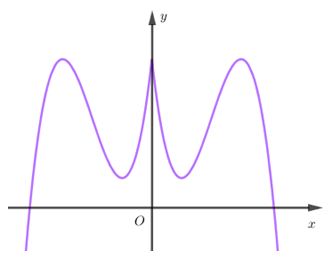
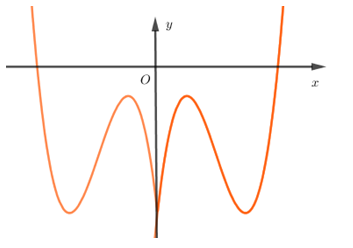
Từ hai đồ thị ở trên ta thấy: Ở cả hai trường hợp thì hàm số \(y = f\left( {\left| x \right|} \right)\) đều có \(5\) điểm cực trị.
Đáp án D







