Câu hỏi
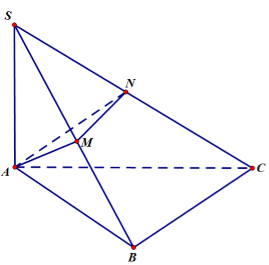
Cho hình chóp S.ABC có\(\left( {SAB} \right),\left( {SAC} \right)\) cùng vuông góc với mặt phẳng đáy, cạnh bên SB tạo với đáy một góc\(60^\circ \) , đáy ABC là tam giác vuông cân tại B với \(BA = BC = a\). Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích của khối đa diện ABMNC
- A \(\dfrac{{\sqrt 3 {a^3}}}{4}\)
- B \(\dfrac{{\sqrt 3 {a^3}}}{6}\)
- C \(\dfrac{{\sqrt 3 {a^3}}}{{24}}\)
- D \(\dfrac{{\sqrt 3 {a^3}}}{8}\)
Phương pháp giải:
- Xác định chiều cao của hình chóp dựa vào định lý: Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng đó.
- Xác định góc giữa đường thẳng \(SB\) và mặt đáy bằng cách xác định góc giữa \(SB\) và hình chiếu của nó trên \(\left( {ABCD} \right)\).
- Tỉ số thể tích giữa hai khối chóp \(S.AMN\) và \(S.ABC\) (\(M,N\) lần lượt thuộc \(SB,SC\)) là \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}}\)
- Áp dụng phương pháp cộng, trừ thể tích để tính thể tích khối đa diện \(ABMNC\).
Lời giải chi tiết:
Cách giải:
Vì \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAC} \right) \bot \left( {ABC} \right)\\\left( {SAB} \right) \cap \left( {SAC} \right) = SA\end{array} \right. \Rightarrow SA \bot \left( {ABC} \right)\)
\(\Rightarrow SA \bot \left( {ABC} \right)\)
\( \Rightarrow AB\) là hình chiếu của \(SB\) trên \(\left( {ABC} \right)\) \( \Rightarrow \widehat {SBA} = {60^0}\)
\(SA = AB\tan {60^0} = a\sqrt 3 \)
\({V_{SABC}} = \dfrac{1}{3}{S_{ABC}}.SA = \dfrac{1}{3}.\dfrac{1}{2}AB.BC.SA = \dfrac{1}{6}{a^3}\sqrt 3 \)
\(\dfrac{{{V_{SAMN}}}}{{{V_{SABC}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = \dfrac{1}{4} \Rightarrow {V_{SAMN}} = \dfrac{1}{4}{V_{SABC}} = \dfrac{1}{{24}}{a^3}\sqrt 3 \)
\( \Rightarrow {V_{ABMNC}} = {V_{SABC}} - {V_{SAMN}} = \dfrac{1}{6}{a^3}\sqrt 3 - \dfrac{1}{{24}}{a^3}\sqrt 3 = \dfrac{{{a^3}\sqrt 3 }}{8}\)
Đáp án D