Câu hỏi
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và khoảng cách A đến mặt phẳng \(\left( {SBC} \right)\) bằng \(\dfrac{{a\sqrt 2 }}{2}\). Tính thể tích V của khối chóp đã cho
- A \(V = \dfrac{{{a^3}}}{2}\)
- B \(V = {a^3}\)
- C \(V = \dfrac{{\sqrt 3 {a^3}}}{9}\)
- D \(V = \dfrac{{{a^3}}}{3}\)
Phương pháp giải:
- Xác định khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng cách xác định hình chiếu của \(A\) lên \(mp\left( {SBC} \right)\).
- Thể tích khối chóp được tính theo công thức \(V = \dfrac{1}{3}Sh\).
Lời giải chi tiết:
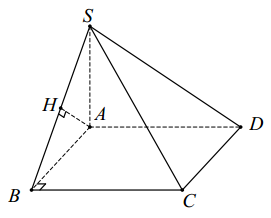
Kẻ đường cao AH của \(\Delta SAB\), ta chứng minh được \(AH \bot \left( {SBC} \right) \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AH\)
\( \Rightarrow AH = \dfrac{{a\sqrt 2 }}{2} = \dfrac{{AB}}{{\sqrt 2 }} \Rightarrow \widehat {SBA} = 45^\circ \Rightarrow SA = AB = a\)
Vậy \({V_{S.ABC{\rm{D}}}} = \dfrac{1}{3}\left( {A{B^2}} \right).SA = \dfrac{{{a^3}}}{3}\)
Đáp án D







