Câu hỏi
Gọi \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\) là hai điểm cực tiểu của hàm số \(y = {x^4} - 2{{\rm{x}}^2} - 3\). Tính \(P = 3{{\rm{x}}_2} + 2{{\rm{x}}_1}\)
- A \(P = - 1\)
- B \(P = 0\)
- C \(P = 1\)
- D \(P = 2\)
Phương pháp giải:
Tính \(y'\), tìm các nghiệm của \(y' = 0\), tìm các điểm cực tiểu \({x_1},{x_2}\) của hàm số và thay vào biểu thức để tính giá trị.
Lời giải chi tiết:
Tập xác định \(D = R\)
Ta có:
\(y' = 4{{\rm{x}}^3} - 4x;y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\)
Bảng biến thiên
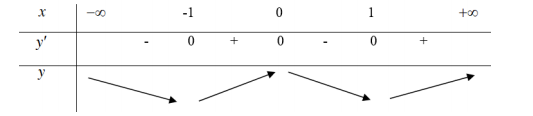
Từ bảng biến thiên ta thấy \({x_1} = - 1\) và \({x_2} = 1\).
Vậy \(P = 1\)
Đáp án C
Câu hỏi trước
