Câu hỏi
Trong không gian cho hình chữ nhật ABCD có AB = 1 và AD = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó.
- A \({S_{tp}} = \dfrac{{4\pi }}{3}\)
- B Stp = 4π
- C Stp = 6π
- D Stp = 3π
Phương pháp giải:
Công thức tính diện tích toàn phần hình trụ: \({S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi r\left( {r + h} \right)\)
Lời giải chi tiết:
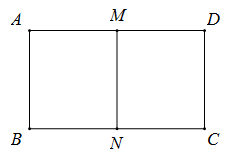
Hình trụ thu được có bán kính đáy r = MA = 1 và chiều cao h = AB = 1
Diện tích toàn phần hình trụ là Stp = 2π r(r + h) = 4π
Chọn đáp án B
Câu hỏi trước
