Câu hỏi
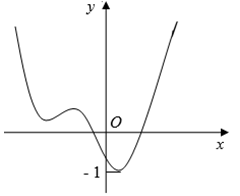
Cho hàm số \(D=R\backslash \left\{ -\frac{1}{c} \right\}.\) có đồ thị như hình vẽ bên
Tìm số điểm cực trị của hàm số \(y={{2}^{f\left( x \right)}}-{{3}^{f\left( x \right)}}.\)
- A 6
- B 5
- C 4
- D 3
Phương pháp giải:
Phương pháp giải:
Tính đạo hàm của hàm số và tìm nghiệm của phương trình \({y}'=0\) dựa vào bài toán tương giao và đồ thị hàm số \(y=f\left( x \right)\) \(\Rightarrow \) Số điểm cực trị của hàm số cần tìm.
Lời giải chi tiết:
Lời giải:
Xét hàm số \(g\left( x \right)={{2}^{f\left( x \right)}}-{{3}^{f\left( x \right)}}\Rightarrow {g}'\left( x \right)={f}'\left( x \right){{.2}^{f\left( x \right)}}.\ln 2-{f}'\left( x \right){{.3}^{f\left( x \right)}}.\ln 3;\,\,\,\forall x\in R\)
Ta có
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\{2^{f\left( x \right)}}.\ln 2 = {3^{f\left( x \right)}}.\ln 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\{\left( {\frac{2}{3}} \right)^{f\left( x \right)}} = \frac{{\ln 3}}{{\ln 2}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\f\left( x \right) = {\log _{\frac{2}{3}}}\frac{{\ln 3}}{{\ln 2}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right..\)
Dựa vào đồ thị hàm số \(y=f\left( x \right),\) ta thấy:
Phương trình \(\left( 1 \right)\) có 3 nghiệm phân biệt (vì hàm số \(y=f\left( x \right)\) có 3 điểm cực trị). Phương trình \(\left( 2 \right)\) vô nghiệm vì đường thẳng \(y={{\log }_{\frac{2}{3}}}\frac{\ln 3}{\ln 2}<-\,1\) không cắt ĐTHS.
Vậy phương trình \({g}'\left( x \right)=0\) có 3 nghiệm phân biệt hay hàm số đã cho có 3 điểm cực trị.
Chọn D