Câu hỏi
Cho hàm số \(y=-{{x}^{4}}+2{{x}^{2}}\) có đồ thị như hình bên.
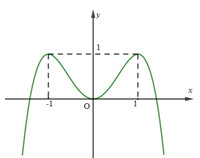
Tìm tất cả các giá trị thực của tham số m để phương trình \(-{{x}^{4}}+2{{x}^{2}}={{\log }_{2}}m\) có 4 nghiệm thực phân biệt.
- A \(m\ge 2.\)
- B \(1<m<2.\)
- C \(0\le m\le 1.\)
- D \(m>0.\)
Phương pháp giải:
Biện luận : Số nghiệm của phương trình \(-{{x}^{4}}+2{{x}^{2}}={{\log }_{2}}m\)bằng số giao điểm của đồ thị hàm số \(y=-{{x}^{4}}+2{{x}^{2}}\) và đường thẳng \(y={{\log }_{2}}m\).
Quan sát đồ thị và đưa ra kết luận.
Lời giải chi tiết:
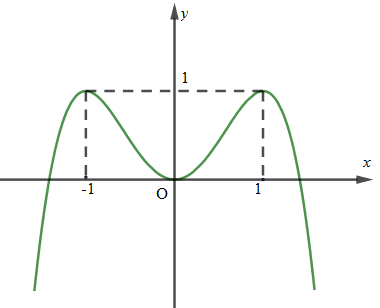
Số nghiệm của phương trình \(-{{x}^{4}}+2{{x}^{2}}={{\log }_{2}}m\)bằng số giao điểm của đồ thị hàm số \(y=-{{x}^{4}}+2{{x}^{2}}\) và đường thẳng \(y={{\log }_{2}}m\).
Do đó, để phương trình \(-{{x}^{4}}+2{{x}^{2}}={{\log }_{2}}m\) có 4 nghiệm thực phân biệt thì \(0<{{\log }_{2}}m<1\Leftrightarrow 1<m<2\)
Chọn B.







