Câu hỏi
Cho hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\) có đồ thị như hình bên. Khẳng định nào sau đây đúng?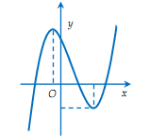
- A \(a,d>0;b,c<0\)
- B \(a,b,d>0;c<0\)
- C \(a,c,d>0;b<0\)
- D \(a,b,c<0;d>0\)
Phương pháp giải:
Quan sát đồ thị và nhận xét.
Lời giải chi tiết:
Ta có hàm số: \(y=a{{x}^{2}}+b{{x}^{2}}+cx+d\)
Từ chiều biến thiên của đồ thị ta có a > 0.
Có: \(y\left( 0 \right)=d>0\)
Đồ thị hàm số có hai điểm cực trị \(\Rightarrow \)phương trình: \(y'\left( x \right)=3a{{x}^{2}}+2bx+c=0\) có hai nghiệm phân biệt \({{x}_{1}}\) và \({{x}_{2}}\) . Chọn \({{x}_{1}}<{{x}_{2}}\)
Mà \({{x}_{1}}<0<{{x}_{2}}\Rightarrow ac<0\Leftrightarrow c<0.\)
Từ đồ thị ta có:
\(\left| {{x}_{1}}-0 \right|<\left| {{x}_{2}}-0 \right|\Rightarrow a+b<0\Leftrightarrow b<-a<0\)
Vậy: \(a,d>0;b,c<0\)
Đáp án A







