Phương pháp giải:

-          Lập bảng xét dấu giá trị tuyệt đối

-          Vẽ đồ thị hàm số với các miền tương ứng

-          Biện luận phương trình dựa vào đồ thị hàm số.

Lời giải chi tiết:

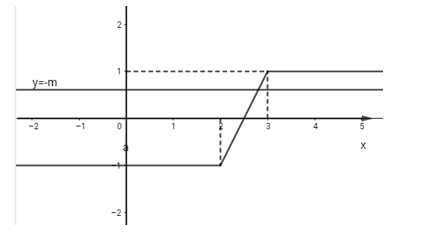
Gọi \(y = |x - 2| - |x - 3|\)

-                               

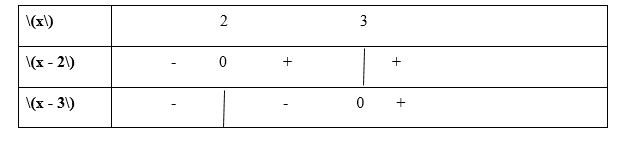
\(y = \left\{ \begin{array}{l} - (x - 2) - ( - x + 3) =  - 1\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{}\end{array}khi}&{x < 2}\end{array}\\(x - 2) - ( - x + 3) = 2x - 5\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{khi}\end{array}}&{}\end{array}}&{2 \le x \le 3}\end{array}\\(x - 2) - (x - 3) = 1\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{\begin{array}{*{20}{c}}{}&{}\end{array}}\end{array}}&{khi}\end{array}\begin{array}{*{20}{c}}{}&{x > 3}\end{array}\end{array} \right.\)

Phương trình \(|x - 1| - |x + 3| =  - m\) có nghiệm duy nhất

\( \Leftrightarrow \)đường thẳng \(y =  - m\)cắt đồ thị hàm số \(y = |x - 1| - |x + 3|\) tại 1 điểm duy nhất\( \Leftrightarrow  - 1 <  - m < 1 \Leftrightarrow \left\{ \begin{array}{l}m < 1\\m >  - 1\end{array} \right. \Leftrightarrow  - 1 < m < 1\).

Chọn C.