Câu hỏi
Điểm sáng A đặt trên trục chính của thấu kính hội tụ có tiêu cự 20 cm, cách thấu kính 30 cm, qua thấu kính cho ảnh A’. Chọn trục tọa độ Ox vuông góc với trục chính, gốc O nằm trên trục chính của thấu kính. Cho A dao động điều hòa theo phương của trục Ox theo quy luật \(x = 4c{\rm{os}}\left( {{\rm{5}}\pi {\rm{t - }}{\pi \over {\rm{3}}}} \right) cm \). Tính từ lúc t = 0, khi A đi hết quãng đường \(S = (54 + 2\sqrt 3 )cm\) thì trên trục Ox ảnh A’ có tọa độ :
- A \( - \sqrt 3 cm\)
- B \( - 4\sqrt 3 cm\)
- C \( 4\sqrt 3 cm\)
- D \( \sqrt 3 cm\)
Phương pháp giải:
Áp dụng công thức thấu kính : \({1 \over d} + {1 \over {d'}} = {1 \over f}\)
Mối liên hệ giữa dao động điều hòa và vòng tròn lượng giác.
Lời giải chi tiết:
Đáp án C
Trả lời:
+ Vị trí ảnh qua thấu kính \(d' = {{df} \over {d - f}} = 60cm\) → ảnh ngược chiều và lớn gấp đôi vật.
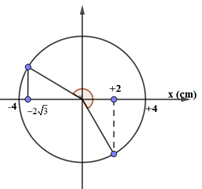
+ Tại thời điểm t = 0, vật đi qua vị trí x = +2 cm theo chiều dương.
+ Sau khi đi được quãng đường 54 cm, vật đến vị trí cân bằng theo chiều âm.
+ Dao động của ảnh ngược pha, biên độ gấp đôi do vậy \({x_{A'}} = 4\sqrt 3 cm\)