Câu hỏi
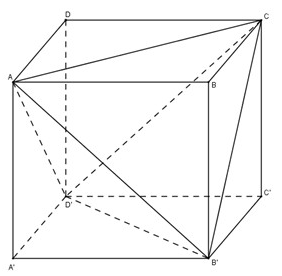
Khối lăng trụ đều ABCD.A’B’C’D’ có thể tích 24cm3. Tính thể tích V của khối tứ diện ACB’D’.
- A \(V = 8\,\,c{m^3}\)
- B \(V = 6\,\,c{m^3}\)
- C \(V = 12\,\,c{m^3}\)
- D \(V = 4\,\,c{m^3}\)
Phương pháp giải:
Phân chia khối lăng trụ đều thành các khối chóp bằng nhau từ đó ta tìm được thể tích của đối tứ diện
Lời giải chi tiết:
Gọi diện tích đáy của lăng trụ là S và h là chiều cao của lăng trụ. Phân chia khối lăng trụ thành khối tứ diện ACB’D’ và 4 khối chóp A.A’B’D’; C.C’B’D’; B’.BAC và D’.DAC. Ta thấy bốn khối chóp sau đều có diện tích đáy bằng S/2 và chiều cao bằng h, nên tổng các thể tích của chúng bằng \(4.\dfrac{1}{3}.\dfrac{S}{2}.h = \dfrac{2}{3}S.h = \dfrac{2}{3}{V_{ABCD.A'B'C'D'}} = \dfrac{2}{3}.24 = 16c{m^3}\)
Khi đó thể tích của tứ diện ACB’D’ là \(\dfrac{1}{3}V = \dfrac{1}{3}.24 = 8\) hoặc 24 – 16 = 8 cm3
Chọn đáp án A.