Phương pháp giải:

Chứng minh thiết diện qua trục là tam giác đều, sử dụng công thức nhanh tính diện tích của tam giác đều cạnh a \(S=\frac{{{a}^{2}}\sqrt{3}}{4}\) và công thức tính diện tích tam giác \(S=\frac{abc}{4R}\), với a, b, c là 3 cạnh của tam giác và R là bán kính đường tròn ngoại tiếp tam giác để tìm ra cạnh của tam giác đều.

Tính chiều cao và bán kính đáy của khối nón, sử dụng công thức \({{l}^{2}}={{h}^{2}}+{{r}^{2}}\), sau đó suy ra thể tích của khối nón \(V=\frac{1}{3}\pi {{r}^{2}}h.\)

Lời giải chi tiết:

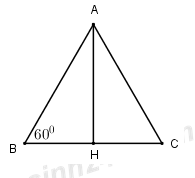
Gọi thiết diện qua trục là tam giác ABC như hình vẽ, hiển nhiên tam giác ABC cân tại A, lại có góc giữa đường sinh và đáy bằng 600 nên \(\widehat{ABC}={{60}^{0}}\). Do đó tam giác ABC đều.

Gọi AB = AC = BC = a, ta có \({{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}}{4R}=\frac{{{a}^{3}}}{4.2}\Leftrightarrow a=2\sqrt{3}\Rightarrow \) \(l=2\sqrt{3}\)

Khi đó \(h=AH=\frac{a\sqrt{3}}{2}=\frac{2\sqrt{3}.\sqrt{3}}{2}=3.\)

Suy ra bán kính đáy hình nón là \(r=\sqrt{{{\left( 2\sqrt{3} \right)}^{2}}-{{3}^{2}}}=\sqrt{3}\)

Vậy \(V=\frac{1}{3}\pi {{r}^{2}}h=\frac{1}{3}\pi {{\left( \sqrt{3} \right)}^{2}}.3=3\pi \)

Chọn B.