Câu hỏi
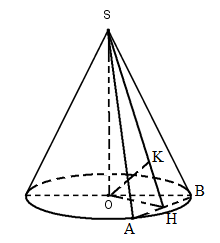
Cho hình nón đỉnh S có chiều cao bằng bán kính đáy và bằng 2a. Mặt phẳng (P) đi qua S cắt đường tròn đáy tại A và B sao cho \(AB=2\sqrt{3}a\). Tính khoảng cách từ tâm của đường tròn đáy đến (P).
- A \(\frac{2a}{\sqrt{5}}\)
- B \(\frac{a}{\sqrt{5}}\)
- C \(a\)
- D \(\frac{a\sqrt{2}}{2}\)
Phương pháp giải:
Dựng khoảng cách từ tâm của mặt đáy đến (P) và tính khoảng cách đó dựa vào các hệ thức lượng trong tam giác vuông.
Lời giải chi tiết:
Gọi O là tâm của đường tròn đáy.
Gọi H là trung điểm của AB ta có \(OH\bot AB\) (quan hệ vuông góc giữa đường kính và dây cung)
Lại có \(SO\bot AB\Rightarrow AB\bot \left( SOH \right).\) Trong mp (SOH) kẻ \(OK\bot SH\) thì \(OK\bot AB\), do đó \(OK\bot \left( SAB \right)\)
\(\Rightarrow d\left( O;\left( P \right) \right)=d\left( O;\left( SAB \right) \right)=OK.\)
Xét tam giác vuông OHB có: \(OH=\sqrt{O{{B}^{2}}-H{{B}^{2}}}=\sqrt{O{{B}^{2}}-\frac{A{{B}^{2}}}{4}}=\sqrt{4{{a}^{2}}-3{{a}^{2}}}=a.\)
Xét tam giác vuông SOH có \(O{{K}^{2}}=\frac{S{{O}^{2}}.O{{H}^{2}}}{S{{O}^{2}}+O{{H}^{2}}}=\frac{4{{a}^{2}}.{{a}^{2}}}{4{{a}^{2}}+{{a}^{2}}}=\frac{4{{a}^{2}}}{5}\Rightarrow OK=\frac{2a}{\sqrt{5}}\).
Chọn A