Phương pháp giải:

Tâm O’ của mặt cầu cần tìm là giao điểm của mặt phẳng trung trực của AB và đường trung trực của SA.

Lời giải chi tiết:

Gọi O’ là giao điểm của mặt phẳng trung trực của AB và đường trung trực của SA.

Vì O’ thuộc của mặt phẳng trung trực của AB nên O’A = O’B = O’M (Với mọi điểm M thuộc đường tròn tâm O), O’ thuộc trung trực của SA nên O’S = O’A, do đó O’A = O’B = O’M = O’S. Vậy O’ là tâm mặt cầu cần tìm.

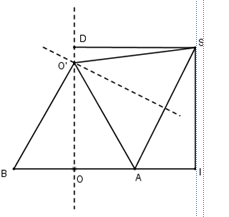
Xét mặt phẳng chứa SI và vuông góc với mp(P) như hình vẽ, dựng hình vuông OISD.

Đặt O’D = x thì OO’ = 2a – x.

Ta có: \(O'S=\sqrt{4{{a}^{2}}+{{x}^{2}}};\,\,O'A=\sqrt{{{a}^{2}}+{{\left( 2a-x \right)}^{2}}}\). Mà O’S = O’A nên

\(\begin{array}{l}\sqrt {4{a^2} + {x^2}} = \sqrt {{a^2} + {{\left( {2a - x} \right)}^2}} \Leftrightarrow 4{a^2} + {x^2} = 5{a^2} - 4ax + {x^2} \Leftrightarrow 4ax = {a^2} \Leftrightarrow x = \frac{a}{4}.\\ \Rightarrow O'S = \sqrt {4{a^2} + {x^2}} = \sqrt {4{a^2} + \frac{{{a^2}}}{{16}}} = \frac{{a\sqrt {65} }}{4} = R.\end{array}\)

Chọn C.