Câu hỏi
Một chất điểm dao động điều hòa trên trục Ox có vận tốc bằng không tại hai thời điểm liên tiếp t1 = 1,75s và t2 =2,5 s, tốc độ trung bình trong khoảng thời gian đó là 16 cm/s. Ở thời điểm t = 0, vận tốc v0 cm/s và li độ x0 cm của vật thỏa mãn hệ thức:
- A $${x_o}{v_o} = - 12\pi \sqrt 3 $$
- B $${x_o}{v_o} = 12\pi \sqrt 3 $$
- C $${x_o}{v_o} = - 4\pi \sqrt 3 $$
- D $${x_o}{v_o} = 4\pi \sqrt 3 $$
Phương pháp giải:
Sử dụng mối liên hệ giữa dao động điều hòa và vòng tròn lượng giác
Lời giải chi tiết:
Đáp án A
Trả lời:
+ Chu kì dao động của vật T = 2(t2 – t1) = 1,5 s
+ $${v_{tb}} = {{2A} \over {\Delta t}} = > A = {{{v_{tb}}\Delta t} \over 2} = 6cm$$
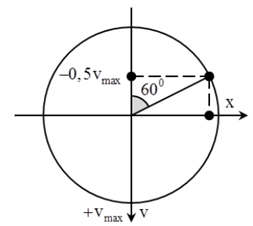
+ Thời điểm t = 0 ứng với góc lùi $$\Delta \varphi = \omega {t_1} = {{7\pi } \over 3} = 2\pi + {\pi \over 3}$$
Từ hình vẽ ta có $${x_0}{v_0} = - {{{v_{max}}} \over 2}{{\sqrt 3 } \over 2}A = - {{\sqrt 3 } \over 4}\omega {A^2} = - 12\pi \sqrt 3 $$
Câu hỏi trước
