Phương pháp giải:

Theo giả thiết \(A'A\) là đường cao. Dùng định lý Py-ta-go để tính \(A'A.\) Áp dụng công thức thể tích lăng trụ để tính thể tích.

Lời giải chi tiết:

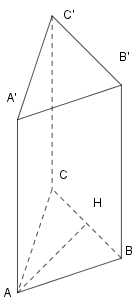
Gọi \(H\) là trung điểm của \(BC.\) Do \(\Delta ABC\) là tam giác cân nên  \(AH\bot BC.\) Mặt khác \(\Delta ABC\) là tam giác vuông nên \(BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=\sqrt{{{4}^{2}}+{{4}^{2}}}=4\sqrt{2},\)

và  \(AH=\frac{1}{2}BC=2\sqrt{2}.\)

Do \(\left\{ \begin{array}{l}{S_{A'BC}} = 16\\{S_{A'BC}} = \frac{1}{2}A'H.BC\end{array} \right. \Rightarrow 16 = \frac{1}{2}A'H.BC \Leftrightarrow A'H = \frac{{16.2}}{{BC}} = \frac{{32}}{{4\sqrt 2 }} = 4\sqrt 2 .\)

Áp dụng định lý Py-ta-go cho tam giác \(\Delta A'AB\) ta có

 \(AA'=\sqrt{A'{{H}^{2}}-A{{H}^{2}}}=\sqrt{{{\left( 4\sqrt{2} \right)}^{2}}-{{\left( 2\sqrt{2} \right)}^{2}}}=2\sqrt{6}.\)

Thể tích là \(V=A'A.{{S}_{ABC}}=\left( 2\sqrt{6} \right).\frac{1}{2}AB.AC=\sqrt{6}.4.4=16\sqrt{6}.\)

Chọn đáp án D