Phương pháp giải:

a) Thực hiện đầy đủ các bước lập BBT và vẽ đồ thị hàm số (P).

b) Để đường thẳng \(y = x + 2m - 1\) cắt đồ thị (P) tại hai điểm phân biệt cùng phía với trục Oy khi và chỉ khi phương trình hoành độ giao điểm có hai nghiệm dương phân biệt.

Lời giải chi tiết:

a) TXĐ: D = R.

Ta có: \( - \frac{b}{{2a}} =  - \frac{{ - 4}}{{2.1}} = 2\) 

Khi x = 2 thì y = -1. (P) có đỉnh \(I\left( {2; - 1} \right)\) và có trục đối xứng x = 2.

a = 1 > 0 nên hàm số đồng biến trên \(\left( {2; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;2} \right)\)

Ta có BBT:

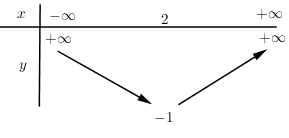
Vẽ đồ thị hàm số:

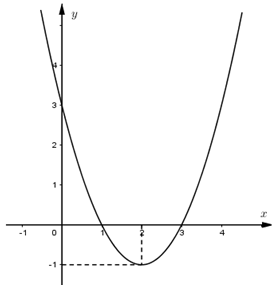
Giao điểm của đồ thị hàm số với trục Ox là (3; 0) và (1; 0)

Giao điểm của đồ thị hàm số với trục Oy là (0; 3).