Câu hỏi
Một hình lăng trụ có đáy là tam giác đều cạnh a, cạnh bên 2a và tạo với đáy góc \({{60}^{\circ }}\) . Ta có thể tích lăng trụ đó bằng:
- A \(\frac{3{{a}^{3}}}{4}\)
- B \(\frac{{{a}^{3}}\sqrt{3}}{9}\)
- C \(\frac{{{a}^{3}}}{4}\)
- D \(\frac{{{a}^{3}}\sqrt{3}}{4}\)
Phương pháp giải:
Xác định chiều cao \(AH\) rồi dùng công thức thể tích lăng trụ để tính thể tích.
Lời giải chi tiết:
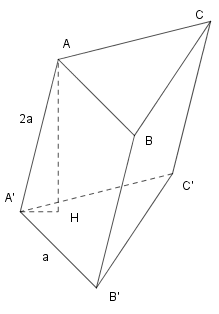
Giả sử lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\) và cạnh bên \(AA'=2a.\) Hạ đường cao \(AH\) xuống mặt phẳng \(\left( A'B'C' \right)\) khi đó theo giả thiết góc giữa cạnh bên và mặt đáy là \({{60}^{0}}\) nên \(\widehat{AA'H}={{60}^{0}}.\) Áp dụng công thức hệ thức lượng trong tam giác ta có \(AH=AA'\sin {{60}^{0}}=2a\frac{\sqrt{3}}{2}=a\sqrt{3}.\)
Thể tích lăng trụ là \(V=AH.{{S}_{A'B'C'}}=a\sqrt{3}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{3{{a}^{3}}}{4}.\)
Chọn đáp án A.
Câu hỏi trước
