Phương pháp giải:

Tính bán kính đáy và đường cao rồi áp dụng công thức thể tích hình nón để tính thể tích.

Lời giải chi tiết:

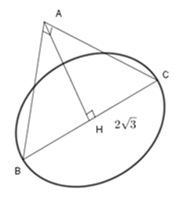
Gọi \(H\) là trung điểm của \(BC\) với \(BC\) là đường kính của đáy. Khi đó \(r=HC=\frac{BC}{2}=\sqrt{3},\,AH\) là đường cao.

Áp dụng định lý Py-ta-go trong tam giác vuông cân \(ABC\) ta có

\(A{{B}^{2}}+A{{C}^{2}}={{\left( 2\sqrt{3} \right)}^{2}}=12\Rightarrow A{{C}^{2}}=\frac{12}{2}=6.\)

Áp dụng định lý Py-ta-go trong tam giác vuông  \(AHC\) ta có

\(A{{H}^{2}}=A{{C}^{2}}-H{{C}^{2}}=6-{{\left( \sqrt{3} \right)}^{2}}=3\Rightarrow AH=\sqrt{3}.\)

Từ đó thể tích của nón là \(V=\frac{1}{3}\pi {{r}^{2}}.AH=\frac{1}{3}\pi {{\left( \sqrt{3} \right)}^{2}}.\sqrt{3}=\pi \sqrt{3}.\)

Chọn đáp án D