Phương pháp giải:

Có hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác dụng vào một vật tại điểm O, khi đó có thể xem vật chịu tác dụng của lực \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} ,\) là hợp lực của hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) được xác định theo quy tắc hình bình hành.

Lời giải chi tiết:

Ta có tổng hợp lực của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) được xác định như hình vẽ.

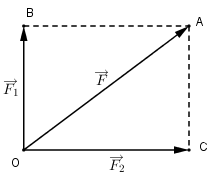
Vì góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng \({90^0}\) nên \(\Delta OAC\) vuông tại C.

Ta có: \(OA = \left| {\overrightarrow F } \right| = 100,AC = \left| {\overrightarrow {{F_1}} } \right| = 60\)

Áp dụng định lí Pi – ta – go ta có: \(AC = \sqrt {O{A^2} - O{C^2}}  = \sqrt {{{100}^2} - {{60}^2}}  = 80.\)

\( \Rightarrow \overrightarrow {{F_2}}  = 80N.\)