Phương pháp giải:

- Đặt phép chia.

- Để thỏa mãn điều kiện của đề bài thì số dư cuối cùng phải chia hết cho số chia. Suy ra, số chia là ước của số dư cuối cùng.

- Lập bảng thử chọn để chọn ra giá trị của thỏa mãn.

Lời giải chi tiết:

\(2{n^3} - 3{n^2} + 3n - 1 = \left( {2{n^2} - n + 2} \right)\left( {n - 1} \right) + 1\)

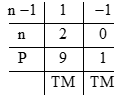
Để \(2{n^3} - 3{n^2} + 3n – 1\) chia hết cho n - 1 thì 1  chia hết cho n - 1.

\( \Rightarrow \left( {n - 1} \right) \in \left\{ {1, - 1} \right\}\)

vậy  \(n = \left\{ {0,2} \right\}\) để  \(P \in Z\)