Câu hỏi
Cho khối lăng trụ tam giác đều ABC.A’B’C’. Một khối trụ T nội tiếp khối lăng trụ đã cho. Gọi là thể tích khối trụ, \({{V}_{2}}\)là thể tích khối lăng trụ. Tính tỉ số \(\frac{{{V}_{1}}}{{{V}_{2}}}\)
- A \(\frac{2\pi \sqrt{3}}{27}\).
- B \(\frac{4\pi \sqrt{3}}{9}\).
- C \(\frac{\pi \sqrt{3}}{9}\).
- D \(\frac{\pi \sqrt{3}}{27}\)
Phương pháp giải:
Tỷ lệ thể tích giữa 1 khối trụ và 1 khối lăng trụ chung chiều cao bằng tỷ lệ diện tích đáy của chúng
Lời giải chi tiết:
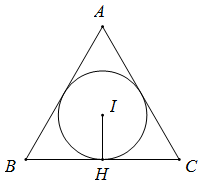
Xét tam giác đều ABC cạnh a có H là trung điểm BC, I là tâm đường tròn nội tiếp tam giác. Diện tích tam giác ABC và hình tròn tâm I lần lượt là S1, S2
\(\begin{array}{l}{S_1} = \frac{{{a^2}\sqrt 3 }}{4}\\IH = \frac{1}{3}AH = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\\{S_2} = \pi I{H^2} = \frac{{\pi {a^2}}}{{12}}\\ \Rightarrow \frac{{{S_2}}}{{{S_1}}} = \frac{{\pi \sqrt 3 }}{9}\end{array}\)
.Đây cũng là tỷ lệ thể tích giữa khối trụ và khối lăng trụ
Chọn đáp án C







