Phương pháp giải:

Phương pháp:

+ Vẽ đồ thị hàm số đã cho

+ Tìm các giá trị nguyên của \(m\) thỏa mãn

Lời giải chi tiết:

Cách giải

Vẽ đồ thị hàm số \(y = \left( {{x^2}-1} \right)\left( {{x^2}-9} \right)\)

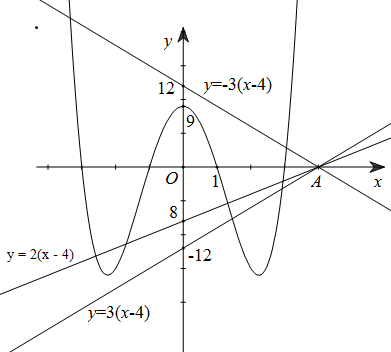
Có \(y' = 4{x^3} - 20x = 0 \Leftrightarrow x = 0;x =  \pm \sqrt 5 \)

Đồ thị hàm số có \(3\)  điểm cực trị \(A\left( {0;9} \right),B\left( { - \sqrt 5 ; - 16} \right),C\left( {\sqrt 5 ;16} \right)\). Đường thẳng \(y = m\left( {x-4} \right)\) luôn đi qua điểm \(A\left( {4;0} \right)\) và điểm \(B\left( {0;-4m} \right)\). Dựa vào đồ thị hàm số:

Ta thấy nếu \(m \geqslant 3\) hoặc \(m \leqslant -3\) thì đường thẳng

\(y = m\left( {x-4} \right)\) cắt đồ thị hàm số đã cho tại nhiều nhất \(2\) điểm.

Khi \(-2 \leqslant m \leqslant 2\)  thì đường thẳng \(y = m\left( {x-4} \right)\) cắt đồ thị hàm số đã cho tại \(4\)  điểm phân biệt

Vậy có \(5\)  giá trị nguyên của \(m\) thỏa mãn.

Chọn đáp án B