Câu hỏi
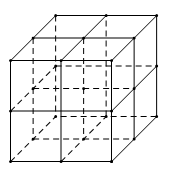
Một khối lập phương có độ dài cạnh là \(2\) cm được chia thành \(8\) khối lập phương cạnh \(1\) cm. Hỏi có bao nhiêu tam giác được tạo thành từ các đỉnh của khối lập phương cạnh \(1\) cm?
- A \(2898\)
- B \(2915\)
- C \(2876\)
- D \(2012\)
Phương pháp giải:
Phương pháp: Tính số đỉnh \(n\) của các hình lập phương cạnh \(1cm\) và tính số tổ hợp chập \(3\) của \(n\) (trừ đi các bộ \(3\) điểm thẳng hàng)
Lời giải chi tiết:
Cách giải
Khi chia hình lập phương cạnh \(2cm\) thành \(8\) hình lập phương cạnh \(1cm\) , số các đỉnh tạo thành là \(9.3 = 27\) (có \(3\) mặt phẳng, mỗi mặt phẳng chứa \(9\) đỉnh)
Chọn \(3\) điểm trong \(27\) điểm trên có \(C_{27}^3 = 2925\) cách
Trong các bộ \(3\) điểm đó, có \(49\) bộ \(3\) điểm thẳng hàng
Vậy số tam giác cần tìm là \(2925-49 = 2876\)
Chọn đáp án C