Câu hỏi
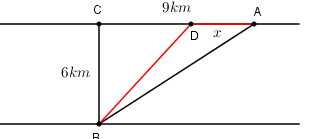
Một công ty muốn làm một đường ống dẫn dầu từ một kho \(A\) ở trên bờ biển đến một vị trí \(B\) trên hòn đảo. Hòn đảo cách bờ biển \(6km.\) Gọi \(C\) là điểm trên bờ sao cho \(BC\) vuông góc với bờ biển. Khoảng cách từ \(A\) đến \(C\) là \(9km.\) Người ta cần xác định một vị trí \(D\) trên \(AC\) để lắp ống dẫn theo đường gấp khúc \(ADB.\) Tính khoảng cách \(AD\) để số tiền chi phí thấp nhất, biết rằng giá để lắp mỗi \(km\) đường ống trên bờ là \(100.000.000\) đồng và dưới nước là \(260.000.000\) đồng.
- A \(7km.\)
- B \(6km.\)
- C \(7.5km.\)
- D \(6.5km.\)
Phương pháp giải:
Đặt \(x=AD.\) Ta thiết lập chi phi theo một hàm của \(x.\) Khảo sát và lập bảng biến thiên cho hàm này trên đoạn \(0<x<9\) để tìm giá trị nhỏ nhất.
Lời giải chi tiết:
Ta đặt \(x=AD.\) Khi đó ta có \(CD=9-x\,\left( km \right).\)
Do \(\Delta BCD\) vuông tại \(C\) nên áp dụng định lý Py-ta-go ta nhận được \(B{{D}^{2}}=B{{C}^{2}}+C{{D}^{2}}={{6}^{2}}+{{\left( 9-x \right)}^{2}}={{x}^{2}}-18x+117\Rightarrow BD=\sqrt{{{x}^{2}}-18x+117}.\)
Chi phí lắp đặt là \(100.000.000x+260.000.000\sqrt{{{x}^{2}}-18x+117}=20.000.000\left( 5x+13\sqrt{{{x}^{2}}-18x+117} \right).\)
Để chi phí là thấp nhất thì ta cần tìm giá trị nhỏ nhất của hàm \(f\left( x \right)=5x+13\sqrt{{{x}^{2}}-18x+117},0<x<9.\)
Ta có
\(\begin{array}{l}f'\left( x \right) = 5 + \frac{{13\left( {x - 9} \right)}}{{\sqrt {{x^2} - 18x + 117} }}.\\\end{array}\)
do đó
\(\begin{array}{l}\,\,\,\,f'\left( x \right) = 0 \Leftrightarrow 5 + \frac{{13\left( {x - 9} \right)}}{{\sqrt {{x^2} - 18x + 117} }} = 0 \Leftrightarrow 5\sqrt {{x^2} - 18x + 117} = 13\left( {9 - x} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}9 - x > 0\\{5^2}\left( {{x^2} - 18x + 117} \right) = {13^2}{\left( {9 - x} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x < 9\\144{x^2} - 2592x + 10764 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 6,5 < 9\\x = 11,5 > 9\end{array} \right..\end{array}\)
Như vậy giá trị \(x=11,5\) bị loại.
Ta kiểm tra được \(f'\left( x \right)>0\) trên \(\left( 6,5;9 \right)\) và \(f'\left( x \right)<0\) trên \(\left( 0;6,5 \right)\) do đó \(f\left( x \right)\ge f\left( 6,5 \right),\,\,\forall x\in \left( 0;9 \right).\)
Như vậy hàm \(f\left( x \right)\) đạt giá trị nhỏ nhất tại \(x=6,5.\)
Khi đó chi phí lắp đặt sẽ nhỏ nhất.
Do đó khoảng cách \(AD\) tìm được khi chi phí thấp nhất là \(6,5km.\)
Chọn đáp án D.